9. Sınıf Matematik Konuları ve Kazanımları
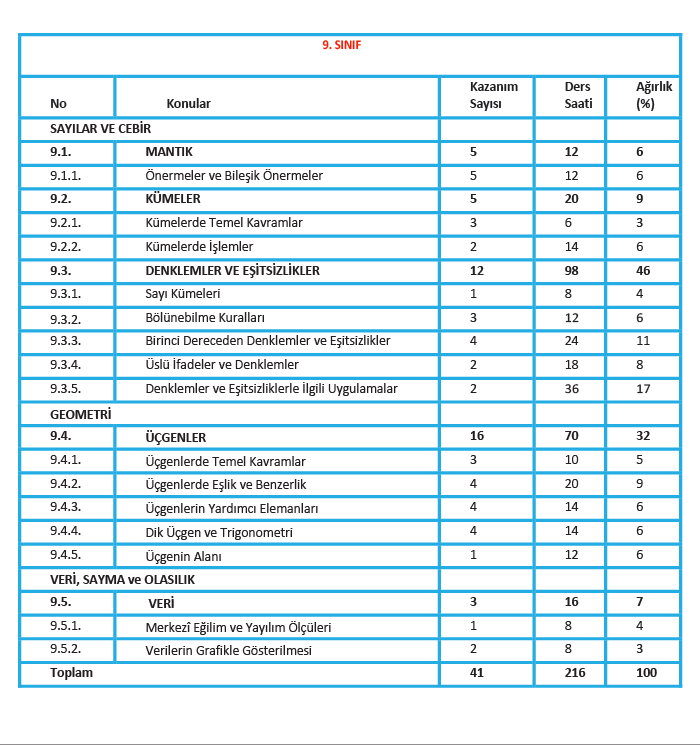
Milli Eğitim Bakanlığı’nın yayımladığı güncel matematik programında yer alan 9. Sınıf Matematik dersi üniteleri, konuları, süreleri ve kazanımları aşağıda verilmiştir.
Konuların üzerine tıklayarak kazanımları görebilirsiniz.
Fen Lisesi 9. sınıf matematik kazanımlarına ulaşmak için tıklayın.
9. Sınıf Matematik Dersi Üniteler ve Zaman Dağılımı Tablosu
Ayrıca, Milli Eğitim Bakanlığı’nın ORTAÖĞRETİM MATEMATİK DERSİ ÖĞRETİM PROGRAMI dosyasına bakabilirsiniz.
MANTIK
- 9.1.1.1. Önermeyi, önermenin doğruluk değerini, iki önermenin denkliğini ve önermenin değilini açıklar.
- 9.1.1.2. Bileşik önermeyi örneklerle açıklar, ‘‘ve, veya, ya da’’ bağlaçları ile kurulan bileşik önermelerin özelliklerini ve De Morgan kurallarını doğruluk tablosu kullanarak gösterir.
- 9.1.1.3. Koşullu önermeyi ve iki yönlü koşullu önermeyi açıklar.
- 9.1.1.4. Her (∀) ve bazı (∃) niceleyicilerini örneklerle açıklar.
- 9.1.1.5. Tanım, aksiyom, teorem ve ispat kavramlarını açıklar.
KÜMELER
- 9.2.1.1. Kümeler ile ilgili temel kavramlar hatırlatılır.
- 9.2.1.2. Alt kümeyi kullanarak işlemler yapar.
- 9.2.1.3. İki kümenin eşitliğini kullanarak işlemler yapar.
- 9.2.2.1. Kümelerde birleşim, kesişim, fark, tümleme işlemleri yardımıyla problemler çözer.
- 9.2.2.2. İki kümenin kartezyen çarpımıyla ilgili işlemler yapar.
DENKLEMLER VE EŞİTSİZLİKLER
- 9.3.1.1. Sayı kümelerini birbiriyle ilişkilendirir.
- 9.3.2.1. Tam sayılarda bölünebilme kurallarıyla ilgili problemler çözer.
- 9.3.2.2. Tam sayılarda EBOB ve EKOK ile ilgili uygulamalar yapar.
- 9.3.2.3. Gerçek hayatta periyodik olarak tekrar eden durumları içeren problemleri çözer.
- 9.3.3.1. Gerçek sayılar kümesinde aralık kavramını açıklar.
- 9.3.3.2. Birinci dereceden bir bilinmeyenli denklem ve eşitsizliklerin çözüm kümelerini bulur.
- 9.3.3.3. Mutlak değer içeren birinci dereceden bir bilinmeyenli denklem ve eşitsizliklerin çözüm kümelerini bulur.
- 9.3.3.4. Birinci dereceden iki bilinmeyenli denklem ve eşitsizlik sistemlerinin çözüm kümelerini bulur.
- 9.3.4.1. Üslü ifadeleri içeren denklemleri çözer.
- 9.3.4.2. Köklü ifadeleri içeren denklemleri çözer.
- 9.3.5.1. Oran ve orantı kavramlarını kullanarak problemler çözer.
- 9.3.5.2. Denklemler ve eşitsizlikler ile ilgili problemler çözer.
ÜÇGENLER
- 9.4.1.1. Üçgende açı özellikleri ile ilgili işlemler yapar.
- 9.4.1.2. Üçgenin kenar uzunlukları ile bu kenarların karşılarındaki açıların ölçülerini ilişkilendirir.
- 9.4.1.3. Uzunlukları verilen üç doğru parçasının hangi durumlarda üçgen oluşturduğunu değerlendirir.
- 9.4.2.1. İki üçgenin eş olması için gerekli olan asgari koşulları değerlendirir.
- 9.4.2.2. İki üçgenin benzer olması için gerekli olan asgari koşulları değerlendirir.
- 9.4.2.3. Üçgenin bir kenarına paralel ve diğer iki kenarı kesecek şekilde çizilen doğrunun ayırdığı doğru parçaları arasındaki ilişkiyi kurar.
- 9.4.2.4. Üçgenlerin benzerliği ile ilgili problemler çözer.
- 9.4.3.1. Üçgenin iç ve dış açıortaylarının özelliklerini elde eder.
- 9.4.3.2. Üçgenin kenarortaylarının özelliklerini elde eder.
- 9.4.3.3. Üçgenin kenar orta dikmelerinin bir noktada kesiştiğini gösterir.
- 9.4.3.4. Üçgenin çeşidine göre yüksekliklerinin kesiştiği noktanın konumunu belirler.
- 9.4.4.1. Dik üçgende Pisagor teoremini elde ederek problemler çözer.
- 9.4.4.2. Öklid teoremini elde ederek problemler çözer.
- 9.4.4.3. Dik üçgende dar açıların trigonometrik oranlarını hesaplar.
- 9.4.4.4. Birim çemberi tanımlar ve trigonometrik oranları birim çemberin üzerindeki noktanın koordinatlarıyla ilişkilendirir.
- 9.4.5.1. Üçgenin alanı ile ilgili problemler çözer.
VERİ
- 9.5.1.1. Verileri merkezî eğilim ve yayılım ölçülerini hesaplayarak yorumlar.
- 9.5.2.1. Bir veri grubuna ilişkin histogram oluşturur.
- 9.5.2.2. Gerçek hayat durumunu yansıtan veri gruplarını uygun grafik türleriyle temsil ederek yorumlar.
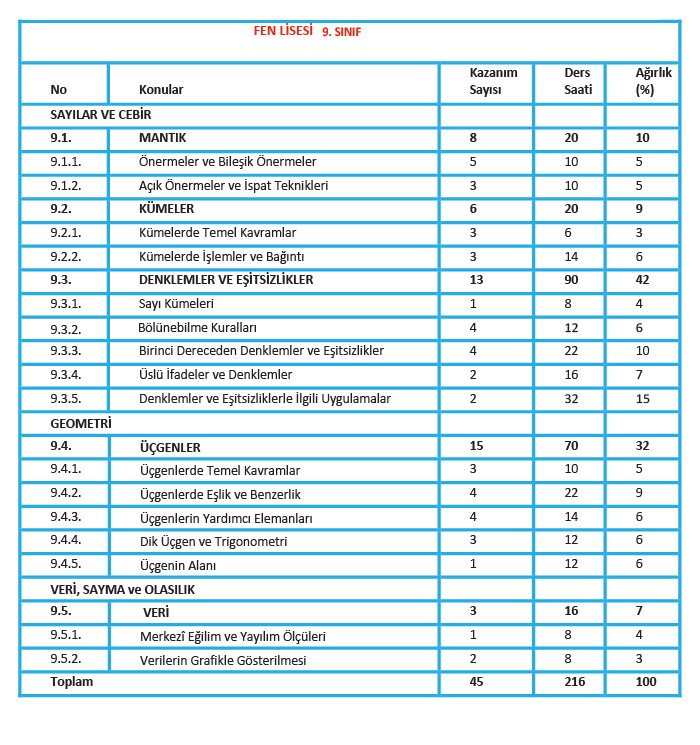
FEN LİSESİ - 9. SINIF MATEMATİK KONULARI VE KAZANIMLARI
FEN LİSESİ - 9. Sınıf Matematik Dersi Üniteler ve Zaman Dağılımı Tablosu
Ayrıca, Milli Eğitim Bakanlığı’nın ORTAÖĞRETİM FEN LİSESİ MATEMATİK DERSİ ÖĞRETİM PROGRAMI dosyasına bakabilirsiniz.
MANTIK
- 9.1.1.1. Önermeyi, önermenin doğruluk değerini, iki önermenin denkliğini ve önermenin değilini açıklar.
- 9.1.1.2. Bileşik önermeyi örneklerle açıklar, ‘‘ve, veya, ya da’’ bağlaçları ile kurulan bileşik önermelerin özelliklerini ve De Morgan kurallarını doğruluk tablosu kullanarak gösterir.
- 9.1.1.3. Koşullu önermeyi ve iki yönlü koşullu önermeyi açıklar.
- 9.1.1.4. Sözel olarak veya sembolik mantık dilinde verilen bileşik önermeleri birbirine dönüştürür.
- 9.1.1.5. Totoloji ve çelişkiyi örneklerle açıklar.9.1.2.1. Her (∀) ve bazı (∃) niceleyicilerini örneklerle açıklar.
- 9.1.2.1. Her (∀) ve bazı (∃) niceleyicilerini örneklerle açıklar.
- 9.1.2.2. Açık önermeyi ve doğruluk kümesini örneklerle açıklar.
- 9.1.2.3. Tanım, aksiyom, teorem ve ispat kavramlarını açıklar.
KÜMELER
- 9.2.1.1. Kümeler ile ilgili temel kavramları hatırlatılır.
- 9.2.1.2. Alt kümeyi kullanarak işlemler yapar.
- 9.2.1.3. İki kümenin eşitliğini kullanarak işlemler yapar.
- 9.2.2.1. Küme işlemleri yardımıyla problemler çözer.
- 9.2.2.2. İki kümenin kartezyen çarpımıyla ilgili işlemler yapar.
- 9.2.2.3. Bağıntı kavramını açıklar.
DENKLEMLER VE EŞİTSİZLİKLER
- 9.3.1.1. Sayı kümelerini birbiriyle ilişkilendirir.
- 9.3.2.1. Tam sayılarda bölünebilme kurallarıyla ilgili problemler çözer.
- 9.3.2.2. Tam sayılardaki bölme algoritması verilir.
- 9.3.2.3. Tam sayılarda EBOB ve EKOK ile ilgili uygulamalar yapar.
- 9.3.2.4. Gerçek hayatta periyodik olarak tekrar eden durumları içeren problemleri çözer.
- 9.3.3.1. Gerçek sayılar kümesinde aralık kavramını açıklar.
- 9.3.3.2. Birinci dereceden denklem ve eşitsizliklerin çözüm kümelerini bulur.
- 9.3.3.3. Mutlak değer içeren birinci dereceden bir bilinmeyenli denklem ve eşitsizliklerin çözüm kümelerini bulur.
- 9.3.3.4. Birinci dereceden iki bilinmeyenli denklem ve eşitsizlik sistemlerinin çözüm kümelerini bulur.
- 9.3.4.1. Üslü ifadeleri içeren denklemleri çözer.
- 9.3.4.2. Köklü ifadeler içeren denklemleri çözer.
- 9.3.5.1. Oran ve orantı kavramlarını kullanarak problemler çözer.
- 9.3.5.2. Denklemler ve eşitsizlikler ile ilgili problemler çözer.
ÜÇGENLER
- 9.4.1.1. Üçgende açı özellikleri ile ilgili işlemler yapar.
- 9.4.1.2. Üçgenin kenar uzunlukları ile bu kenarların karşılarındaki açıların ölçülerini ilişkilendirir.
- 9.4.1.3. Uzunlukları verilen üç doğru parçasının hangi durumlarda üçgen oluşturduğunu değerlendirir.
- 9.4.2.1. İki üçgenin eş olması için gerekli olan asgari koşulları değerlendirir.
- 9.4.2.2. İki üçgenin benzer olması için gerekli olan asgari koşulları değerlendirir.
- 9.4.2.3. Üçgenin bir kenarına paralel ve diğer iki kenarı kesecek şekilde çizilen doğrunun ayırdığı doğru parçaları arasındaki ilişkiyi kurar.
- 9.4.2.4. Üçgenlerin benzerliği ile ilgili problemler çözer.
- 9.4.3.1. Üçgenin iç ve dış açıortaylarının özelliklerini elde eder.
- 9.4.3.2. Üçgenin kenarortaylarının özelliklerini elde eder.
- 9.4.3.3. Üçgenin kenar orta dikmelerinin bir noktada kesiştiğini gösterir.
- 9.4.3.4. Üçgenin çeşidine göre yüksekliklerinin kesiştiği noktanın konumunu belirler.
- 9.4.4.1. Dik üçgende Pisagor teoremini elde ederek problemler çözer.
- 9.4.4.2. Öklid teoremini elde ederek problemler çözer.
- 9.4.4.3. Dik üçgende dar açıların trigonometrik oranlarını hesaplar.
- 9.4.4.4. Birim çemberi tanımlar ve trigonometrik oranları birim çemberin üzerindeki noktanın koordinatlarıyla ilişkilendirir.
- 9.4.5.1. Üçgenin alanı ile ilgili problemler çözer.
VERİ
- 9.5.1.1. Verileri merkezî eğilim ve yayılım ölçülerini hesaplayarak yorumlar.
- 9.5.2.1. Bir veri grubuna ilişkin histogram oluşturur.
- 9.5.2.2. Gerçek hayat durumunu yansıtan veri gruplarını uygun grafik türleriyle temsil ederek yorumlar.